Menu

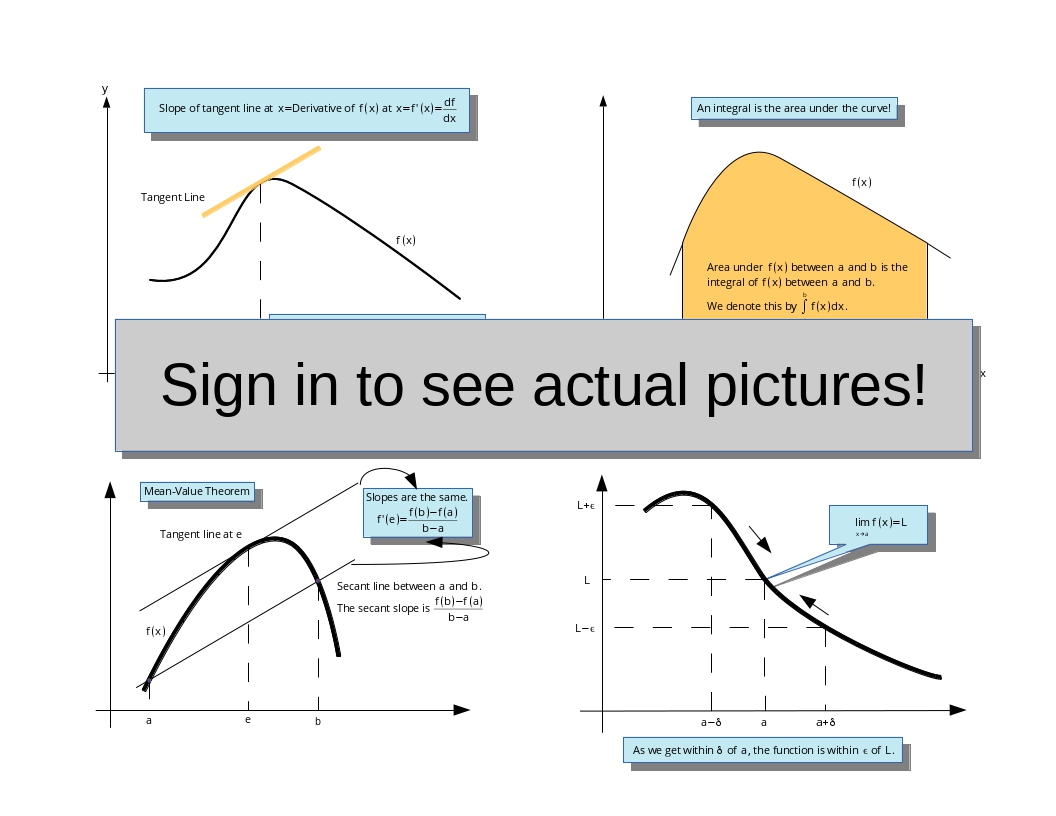
Prove that if $f(x)$ is continuous on $[a,b]$ and we have a point $e$ such that $a\lt e\lt b$, then \begin{eqnarray}&&\int_a^b\,f(x)dx\\&=&\int_a^e\,f(x)dx+\int_e^b\,f(x)dx.\end{eqnarray}

Primary tabs

Lesson Parent:

Integration III: Definite Integrals As Upper and Lower Sums

Problem:

Prove that if $f(x)$ is continuous on $[a,b]$ and we have a point $e$ such that $a\lt e\lt b$, then
\begin{equation}
\int_a^b\,f(x)dx=\int_a^e\,f(x)dx+\int_e^b\,f(x)dx.
\end{equation}

Answer:

It is true that if $f(x)$ is continuous on $[a,b]$ and we have a point $e$ such that $a\lt e\lt b$, then \begin{equation} \int_a^b\,f(x)dx=\int_a^e\,f(x)dx+\int_e^b\,f(x)dx. \end{equation}

Solution:

What we are wanting to prove is that the area under a function $f(x)$ can be broken into pieces. The area of the whole is the sum of the areas broken into two pieces:

Recall our definition of a definite integral using upper and lower sums. In that definition

<Sign in to see all the formulas>

is true for every possible partition of $[a,b]$. Therefore, to prove that

<Sign in to see all the formulas>

we must show that

<Sign in to see all the formulas>

for every possible partition.

From our notation above, we have $P$ being a partition of the x-axis and $L(P)$ and $U(P)$ being upper and lower sums such that

<Sign in to see all the formulas>

We can add the point $e$ to $P$ to create partition $Q$. Furthermore, we know that

<Sign in to see all the formulas>

Now let's recall that

<Sign in to see all the formulas>

Since the partition $Q$ contains the point $e$, we can break $L(Q)$ into two parts. One part where the intervals in the partition are in $[a,e]$ and the part where the intervals in the partition are in $[e,b]$. Let's say that the point $x_j=e$ so we can write

<Sign in to see all the formulas>

where $Q_a$ is a partition with all the points of $Q$ in $[a,e]$ and $Q_b$ is a partition with all the points of $Q$ in $[e,b]$. (Math afficionados would say <Sign in to see all the formulas> and <Sign in to see all the formulas>.) We also find the same thing for the upper sum $U(Q)$ so that

Prove that if $f(x)$ is continuous on $[a,b]$ and we have a point $e$ such that $a\lt e\lt b$, then \begin{eqnarray}&&\int_a^b\,f(x)dx\\&=&\int_a^e\,f(x)dx+\int_e^b\,f(x)dx.\end{eqnarray}

Primary tabs

SAMPLE SOLUTION

GAIN AN ADVANTAGE